
Mastering PSLE Mathematics: Guide to Maths Heuristics for PSLE
The Primary School Leaving Examination (PSLE) in Singapore is a significant milestone for every primary school student, with mathematics being one of the core subjects assessed. Mastering PSLE mathematics requires not only understanding concepts but also being good at problem-solving strategies.
One essential aspect of PSLE maths is the application of heuristics, which are problem-solving techniques that help students approach and solve complex mathematical problems more effectively. In this guide, we’ll delve into various maths heuristics tested in the PSLE exam, providing diagrams, worked examples, and practical tips for parents to support their children’s learning at home.
Understanding Maths Heuristics
Maths heuristics are systematic problem-solving strategies that enable students to tackle mathematical problems methodically. These heuristics guide students in breaking down complex problems into manageable steps, identifying relevant information, and applying appropriate mathematical concepts to find solutions. By mastering maths heuristics, students can approach a wide range of mathematical problems with confidence and accuracy.
1. Model Drawing
Model drawing is a powerful heuristic that involves representing mathematical problems visually using diagrams or models. This strategy helps students visualise the problem, identify key information, and formulate a plan to solve it systematically. Model drawing is particularly useful for solving word problems involving fractions, ratios, and comparison.
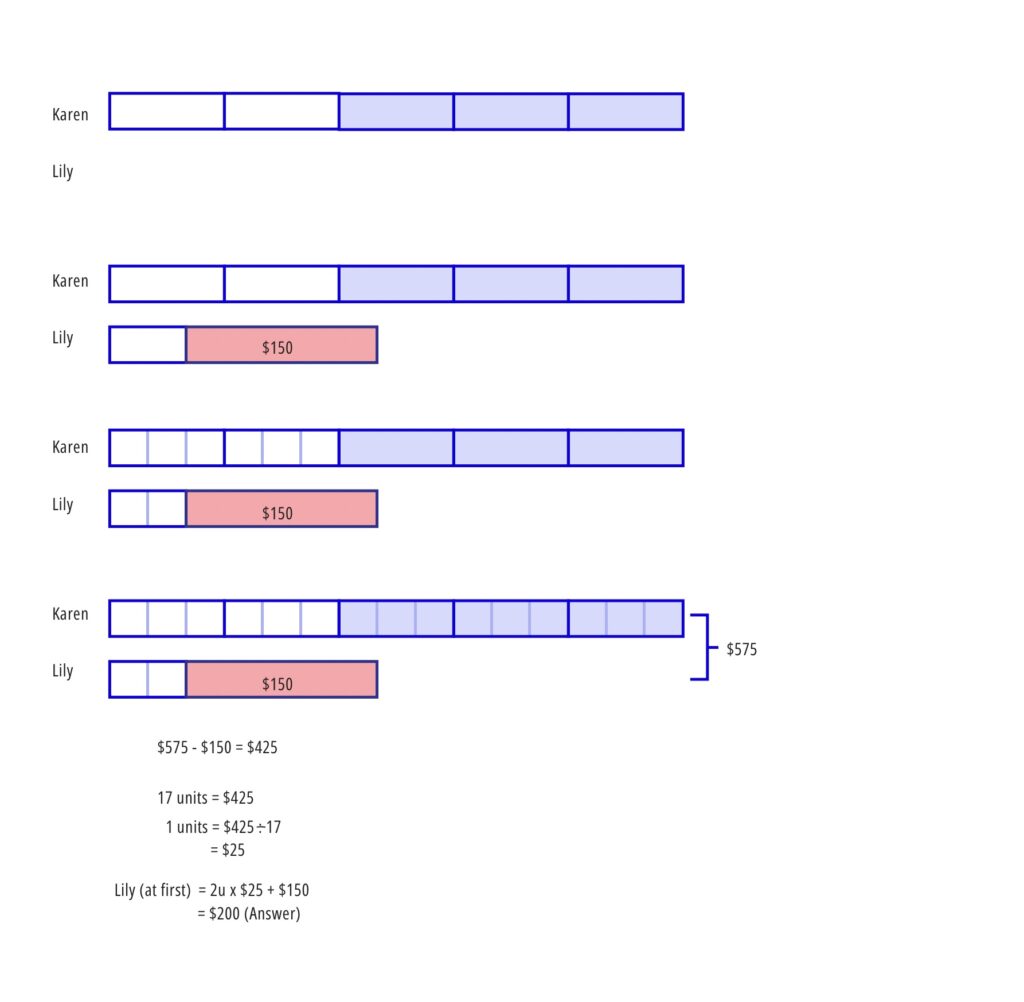
Example: Karen and Lily had $575 altogether. Karen spent 3/5 of his money and Lily spent $150. Karen then had three times as much money as Lily. How much did Lily have at first?
Solution:
2. Guess and Check
Guess and check involves making educated guesses and testing them systematically to determine if they are correct. This encourages students to use trial and error to approach problems, refining their guesses based on feedback until they find the correct solution. Guess and check is particularly useful for problems involving logical reasoning and estimation.
Example: Find a two-digit number where the sum of its digits is 9, and the number is greater than 50.
Solution:

3. Work Backwards
Work backwards involves starting with the desired outcome and working backwards to determine the steps needed to achieve it. This encourages students to think logically and consider the relationship between different elements of a problem. Working backwards is particularly useful for problems involving sequences, patterns, and algebraic equations.
Example 1:
Jack has 20 more marbles than Sam. Together, they have 80 marbles. How many marbles does Jack have?

Example 2:
Sarah had some pencils. She gave Jason 15 pencils and then bought 1 more pencil. She then gave Sam 12 pencils and bought another 2 pencils. If she had 6 pencils left in the end, how many pencils did Sarah have at first?
Solution:
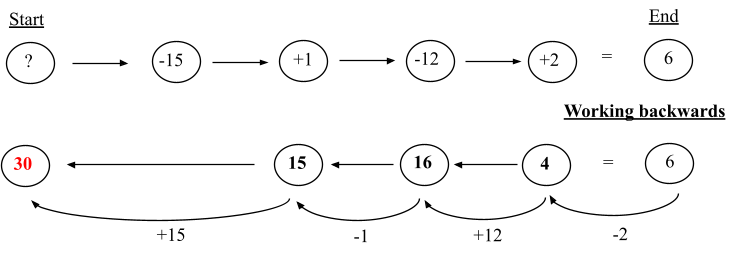
Explanation:
From start to end,
- Sarah gave Jason 15 pencils = -15
- Sarah gave Sam 12 pencils = -12
- Sarah bought 3 pencils = +1 and +2
Working backwards,
- we begin with the number of pencils Sarah ended with which is 6.
- Since she bought 2 pencils, we subtract 2 from 6 to get 4.
- Then, we add 10 to 4 because she gave 10 pencils to Sam to get 14.
- Again, subtract 1 from 14 to get 13.
- Lastly, we add 22 to 13 to obtain 35 pencils that Sarah had originally.
4. Look for a Pattern
Looking for a pattern involves identifying recurring sequences or relationships within a problem to find a solution. This encourages students to analyse data, observe trends, and make connections between different elements of a problem. Looking for a pattern is particularly useful for problems involving sequences, geometric shapes, and number patterns.
Example: What is the next number in the sequence: 2, 6, 12, 20, …?
Solution:

5. Systematic Listing
Systematic listing involves organising information systematically to analyse all possible outcomes and find a solution. This encourages students to use tables, charts, or lists to organise data and identify patterns or relationships. Systematic listing is particularly useful for problems involving permutations, combinations, and probability.
Example 1:
How many different three-letter combinations can be formed using the letters A, B, C, and D?
Solution:
List the combinations systematically starting with ‘A’ followed by ‘B’, ‘C’ and then ‘D’.

There are 24 combinations.
Example 2:
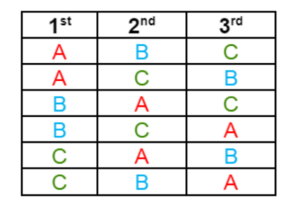
Andy, Bill and Colin are competing in a running race. List all the possible finishing positions for the 3 runners.
Solution:
Represent each person with an alphabet:
- Andy = A
- Bill = B
- Colin = C
Practical Tips for Parents to Guide Their Kids at Home
Practice Regularly: Encourage your child to practice maths heuristics regularly through worksheets, online resources, or maths games. Repetition helps reinforce problem-solving strategies and builds confidence in tackling different types of problems.
Provide Feedback: Offer constructive feedback and praise your child’s efforts in applying math heuristics. Focus on the process rather than just the outcome, highlighting their problem-solving approach and critical thinking skills.
Encourage Persistence: Emphasise the importance of perseverance and resilience when facing challenging maths problems. Encourage your child to approach problems systematically, try different strategies, and learn from mistakes.
Make it Fun: Incorporate maths heuristics into everyday activities and games to make learning enjoyable. Explore real-life scenarios, puzzles, and brainteasers that require problem-solving skills and critical thinking.

Mastering PSLE mathematics requires more than just memorising formulas and procedures—it involves developing effective problem-solving strategies and critical thinking skills. By understanding and applying maths heuristics such as model drawing, guess and check, work backwards, look for a pattern, and systematic listing, students can approach PSLE maths questions with confidence and accuracy.
By providing guidance, encouragement, and opportunities for practice, in:genius by Nascans can help your child develop the skills and confidence needed to excel in PSLE mathematics and beyond.



